
Neste material trazemos algumas sugestões para trabalhar as noções presentes no estudo da Probabilidade nos Anos Inicias do Ensino Fundamental.
Conteúdos
Noções de aleatoriedade e chance, Espaço amostral, Noções de possibilidade e probabilidade
Objetivos
Ao final dessa sequência, espera-se que as crianças:

Aprendendo probabilidade com cartões coloridos
1. Quem tem mais chance?
Para realizar essa sequência de atividades você precisará de uma caixa ou uma sacola opaca e 24 cartões do mesmo tamanho e de mesma espessura, sendo 15 amarelos, 7 azuis e 2 vermelhos. Antes de colocar os cartões dentro da sacola, mostre-os para as crianças e convide-as a contar e comparar os cartões, a pensar qual cor aparece mais e qual aparece menos. Depois dessa análise, guarde todos os cartões na sacola e explique para elas que vocês farão vários experimentos para descobrir o que é ou não possível acontecer e quais as chances de determinadas situações acontecerem no sorteio dos cartões coloridos.
Em seguida, organize uma roda de conversa e faça algumas perguntas para as crianças. Essa primeira atividade é um tipo de sondagem inicial. Ela é interessante porque põe as crianças em contato com uma situação real em que precisam usar seus conhecimentos prévios a respeito das noções de chance e aleatoriedade. Faça outros sorteios, sempre devolvendo os cartões a cada rodada, para garantir que as chances sejam as mesmas. Incentive-os a explicar o que está ocorrendo.
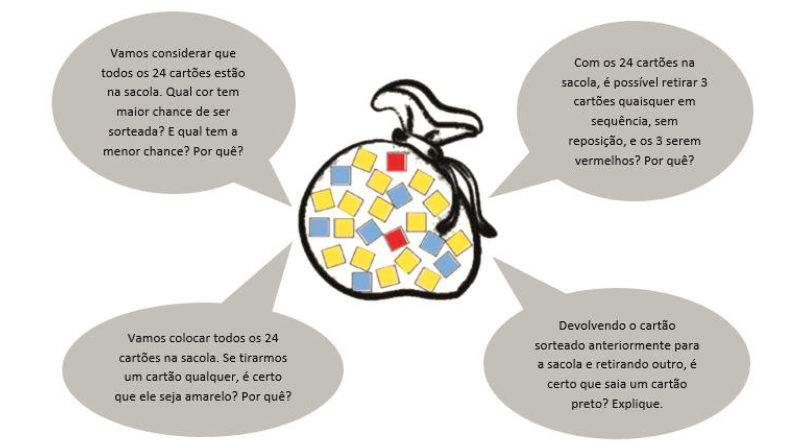
Amplie as perguntas e incentive as crianças a levantar outras hipóteses. Faça outros sorteios, sempre devolvendo os cartões a cada rodada, para garantir que as chances sejam as mesmas. Incentive-as a explicar o que está ocorrendo. É importante que as crianças percebam que mesmo tendo mais cartões amarelos, pode acontecer de sair cartões da cor azul ou vermelha. Isso significa que é muito possível que saia um cartão amarelo, possível que saia um cartão azul, pouco possível que saia um cartão vermelho e impossível que saia um cartão preto.
Observação: Caso você não tenha esse recurso de papel colorido, pode substitui-lo por papel sulfite branco e escrever o nome das cores, usar bolinhas de papel (jornais, revistas) ou grãos (feijão, milho, canjica, entre outros).
2. Sorteando cartões: Eventos possíveis ou prováveis?
Para ajudar as crianças na compreensão das ideias de eventos possíveis ou prováveis, bem como na análise desses eventos, vamos conhecer a próxima atividade, que pode ser realizada individualmente ou em pequenos grupos. Entregue para cada criança uma cópia da ficha com quatro propostas de análise, conforme o modelo a seguir:
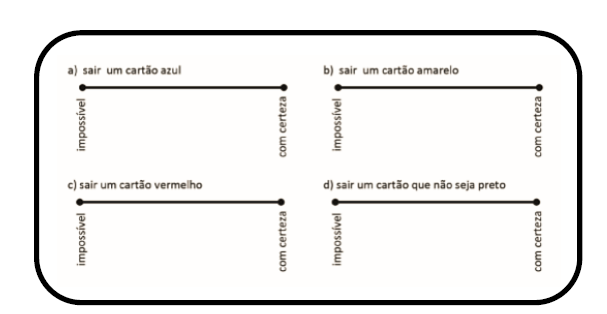
Em seguida explique a elas que essas linhas funcionarão como termômetros, onde iremos marcar o que achamos possível, impossível ou certo que irá acontecer em cada evento, ou seja, em cada acontecimento. Se tivermos certeza, faremos uma marca sobre o ponto “com certeza” e se for impossível, a marca será feita sobre o ponto “impossível”. Mas se o resultado for apenas possível, como fazer as marcas nas linhas?
Observe nas linhas abaixo o que quatro crianças pensaram e marcaram sobre o evento “sair um cartão azul”:
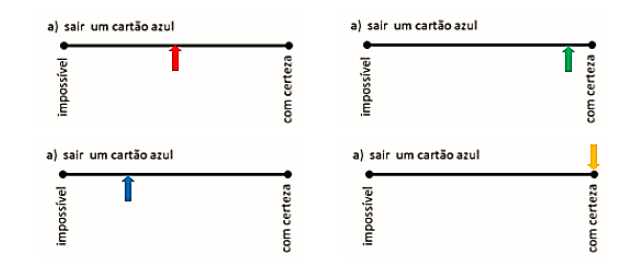
Observe que cada criança marcou um ponto em um local diferente da reta. Apenas uma delas acertou. Qual delas? O que será que ela pensou para chegar a essa conclusão?
Em sala de aula, você pode questionar as crianças sobre essas situações e ver como elas lidam com a possibilidade de o evento em questão estar mais próximo ou mais afastado de determinada extremidade. Deixe que elas cheguem a conclusão, por exemplo, de que se a chance de sair um cartão amarelo é bem maior do que de sair um cartão vermelho, então, ao analisar o evento do item B, a marca precisa ser feita mais próxima do “com certeza”, enquanto no evento do item C a marca precisa estar mais próxima do “impossível”. Invista em boas análises!
3. Analisando e organizando os cartões coloridos: O espaço amostral
A próxima atividade convida as crianças a fazerem análises associadas a descrição do espaço amostral. O foco está centrado no desenvolvimento da noção de espaço amostral, não nas resoluções das situações propostas, mas sim nos elementos envolvidos nas situações probabilísticas, na ideia de possibilidades. É comum que as crianças dos Anos Iniciais não conheçam o termo espaço amostral, mas podem compreender a ideia, especialmente em experiências como a que propomos aqui. Por isso é importante valorizar a oralidade nessa fase.
Assim como na atividade anterior, as crianças podem ser organizadas individualmente ou em pequenos grupos. Distribua para cada criança uma cópia com quarto propostas de análise e organização do espaço amostral, conforme o modelo abaixo:
As sacolas estão vazias e você escolhe quantos cartões irá colocar dentro delas, desde que suas escolhas garantam que os eventos indicados se realizem. Lembre-se que você tem os 24 cartões (15 amarelos, 7 azuis e 2 vermelhos). Desenhe as possíveis soluções:
Com certeza será sorteado um cartão vermelho. É muito possível que seja sorteado um cartão amarelo.
É impossível ser sorteado um cartão azul. É pouco possível que seja sorteado um cartão verde.
4. Qual é a probabilidade?
Chegou o momento de calcular probabilidades. Até aqui as crianças já vivenciaram situações em que precisaram relacionar a quantidade de casos favoráveis e possíveis de maneira intuitiva e analítica.
Vamos fazer uma retomada e identificar quem é quem nas atividades? Na atividade 1, os cartões representam o espaço amostral de um experimento aleatório. Na atividade 2, analisamos eventos possíveis ou prováveis, certos ou impossíveis. Definimos como evento qualquer subconjunto do espaço amostral, como por exemplo “sair um cartão amarelo”. Na atividade 3 fizemos uma análise sobre como organizar o espaço amostral para garantir que os eventos se realizassem.
Essas propostas abriram caminho para iniciarmos o trabalho com o cálculo dessa relação chamada probabilidade, a razão entre o número de casos favoráveis e o número de casos possíveis. O número de casos favoráveis nada mais é que a quantidade de elementos de determinado evento, enquanto o número de casos possíveis refere-se à quantidade de elementos do espaço amostral. Para isso, vamos voltar ao início dessa sequência e analisar a sacola com os 24 cartões coloridos. Analise e responda as perguntas abaixo.
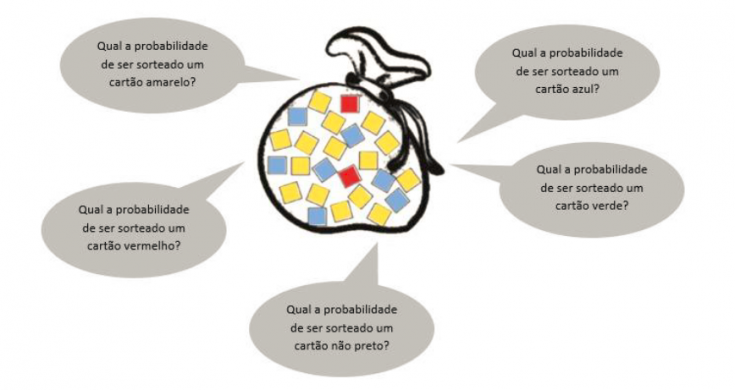
A partir das ideias e noções trabalhadas até aqui, vamos analisar a primeira pergunta:
“Qual a probabilidade de ser sorteado um cartão amarelo?”
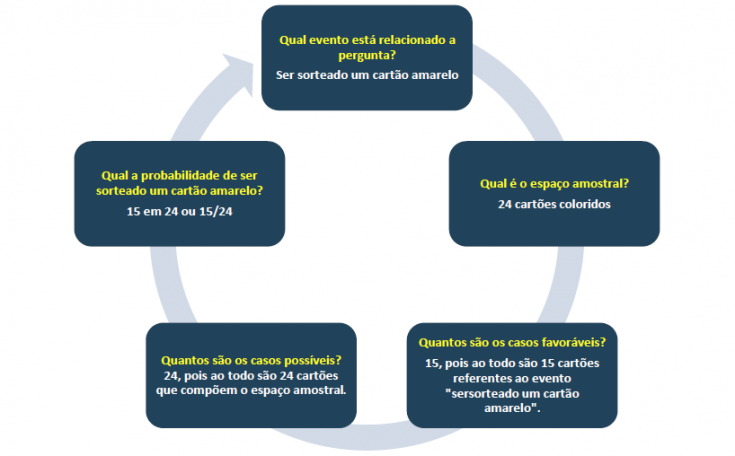
Ressalte a importância dessas ideias concluindo com as crianças que para calcular probabilidade é preciso analisar cada situação, com atenção aos elementos que ajudam nessa análise, identificar os eventos prováveis e possíveis e relacioná-los, comunicando essa resposta, inicialmente, na forma fracionária.
REFERÊNCIAS
● BRASIL. Conselho Nacional de Educação; Câmara de Educação Básica. Resolução CNE/CP nº 2, de 22 de dezembro de 2017. Base Nacional Comum Curricular, dezembro, 2017. Disponível em: http://basenacionalcomum.mec.gov.br/a-base/ (acesso em 02/03/2018).
● Geromel Meneghetti, Renata C.; de Fátima Batistela, Rosemeire; Viggiani Bicudo, Maria Aparecida. A Pesquisa sobre o Ensino de Probabilidade e Estatística no Brasil: um exercício de metacompreensão. Boletim de Educação Matemática, vol. 24, n. 40, dezembro, 2011, pp. 811-833. Universidade Estadual Paulista Júlio de Mesquita Filho. Rio Claro, Brasil.
● LOPES, Celi Espasandim. O ensino da Estatística e da Probabilidade na Educação Básica e a Formação de Professores. Caderno CEDES vol 28, n. 74. Campinas, 2008.
● SMOLE, Katia Stocco; DINIZ, Maria Ignez (orgs). Caderno de formação: Probabilidade Anos Iniciais. São Paulo: Edições Mathema, 2019.
● VAN DE WALLE, John A. Matemática no ensino fundamental Formação de professores e aplicação em sala de aula. Porto Alegre: Artmed, 2009.
Todos os campos devem ser preenchidos.
Seu e-mail não será publicado.
Esse texto se faz relevante pois nos orienta a trabalhar eventos do cotidiano que podem ser influenciados pela sorte para que a criança entenda as possibilidades : mais prováveis, menos prováveis…
Boa tarde!
Na prática já estamos iniciando este trabalho nos anos iniciais (1º e 2º anos principalmente), com a noção de chance e aleatoriedade, e aos poucos, vamos avançando especificando nos próximos anos, até chegarmos nos cálculos com os 4º e 5º anos. As vezes, o que sinto que falta lá nos 5º anos é fazer a relação dessa noção que foi desenvolvida nos anos anteriores com uma retomada para o brincar, sortear, para fazer relembrá-los e não apenas, focar no cálculo da probabilidade, e assim, unificar o aprendizado dando sentido.
Texto muito bem explicado e informativo sobre como ensinar Probabilidades.
O uso de jogos como recurso pedagógico para o ensino da Probabilidade possibilita o desenvolvimento de forma particular de pensamento e raciocínio além de certas atitudes que possibilitam o posicionamento crítico, o fazer previsões e o tomar decisões, de maneira lúdica. É um desafio único que provoca nos alunos o calcular de maneira mais prazerosa.
Achei as propostas muito interessantes e ampliaram o meu conhecimento sobre o assunto.
Texto muito esclarecedor.
Parabéns!
Na minha opinião o texto atinge o seu papel que é trabalhar probabilidade.
Excelente!
Realmente se faz necessário inserir a probabilidade no ensino da matemática, acredito que seria interessante ter mais cursos voltados a esse tema principalmente nas faculdades onde se aprende muita teoria ,pouca prática .
Todo o trabalho a ser desenvolvido foi muito bem explicado. Agradeço a toda a equipe por nos proporcionar um material tão esclarecedor.