MATEMÁTICA E DOSAGEM DE MEDICAMENTOS

Objetivos

• Ler, escrever, comparar e ordenar números naturais pela compreensão das características do Sistema de Numeração Decimal;
• Produzir escritas numéricas reconhecendo o valor posicional da unidade, dezena, centena e unidade de milhar;
• Compor e decompor números naturais;
• Interpretar, produzir e comparar escritas numéricas;
• Resolver problemas que envolvam a análise do valor de um algarismo conforme a posição que ocupa em um número;
• Utilizar as propriedades aditivas e multiplicativas do sistema de numeração posicional decimal para resolver problemas que envolvam compor e decompor números.

Recomendação

Alunos a partir de 13 anos

Organizado por

Maria Ignez Diniz, diretora do Mathema

Materiais

• Garrafa PET, sucata, dosadores, colheres, xícaras;
• Calculadora simples para cada dupla de alunos.

Sugestão das aulas

Leia com atenção toda a atividade porque na 1ª parte será necessária a observação e coleta de informações pelos jovens em suas casas e, para a 3ª parte, será preciso providenciar com antecedência alguns objetos para que a atividade aconteça adequadamente.

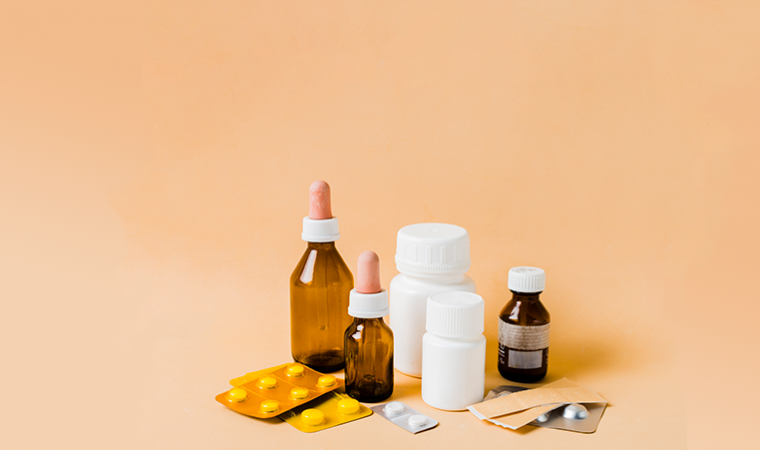
Converse com a classe sobre a importância da exatidão nas medições na dosagem de medicamentos. Certamente eles devem ter notícias sobre casos de erros no uso de remédios que podem ter gerado danos à saúde de pessoas ou de animais domésticos.

1ª parte

Prepare uma apresentação com imagens de rótulos de alguns medicamentos, como os que se seguem e, com a classe em roda, questione:

• Vocês conhecem esses medicamentos ou algum parecido?
• Quais informações desses rótulos indicam a quantidade do medicamento?
• O que acham que significam as expressões 2 mg/5 mL e 3,0 mg/mL?
• Qual o sentido da informação 1.200.000 U ou 600.000 unidades em embalagens do mesmo medicamento?

 

 

Permita que exponham suas hipóteses e concordem ou não uns com os outros.

Em seguida, apresente o conceito de concentração, que é muito importante para a dosagem de medicamentos, uma vez que é ela que determina a quantidade do agente ativo dissolvido em água ou de outro produto usado para dissolver o componente que realmente pode ser chamado de remédio para determinada enfermidade.

 

Vamos introduzir a terminologia e os conceitos básicos relativos a soluções:

Solvente é a parte líquida da solução na qual o elemento principal está dissolvido. Normalmente, é água destilada.

Soluto é a porção sólida da solução, ou seja, se toda a parte líquida se evaporasse, o que sobraria seria o soluto. No caso do soro fisiológico, o que sobraria seria o cloreto de sódio.

Concentração é a relação entre a quantidade de massa do soluto e o volume total da solução. No caso do anti-histamínico, a concentração é de 2 mg/5 mL. Isso significa que em cada 5 mL da solução, encontram-se 2 mg do composto ativo de maleato de dexclorfeniramina.

Informe os jovens de que há outras maneiras de indicar a concentração em um medicamento:

1. Em porcentagem − por exemplo, 0,9% ou 12% significa que em cada 100 partes da solução, 0,9 partes ou 12 partes são do soluto.
2. Em proporção − por exemplo, 1:100 ou 1:1000, como na concentração de uma ampola de adrenalina. Nesses casos, significa que há uma parte de soluto em 100 partes ou 1000 partes da solução.
3. Em unidades − como encontramos 1.200.000 U ou 100 UI/mL. U ou UI é uma unidade padronizada internacionalmente cujo valor em gramas varia de acordo com a substância.

 

Estabelecidas as primeiras ideias, depois dessa breve abordagem sobre as unidades que aparecem nos medicamentos que são soluções, solicite que os alunos pesquisem em suas casas os rótulos de medicamentos que são soluções e anotem, de modo organizado, as informações que encontrarem. Isso pode ser feito em uma tabela com o nome do medicamento, a concentração encontrada no rótulo e o volume líquido do frasco, por exemplo:

 

 

É importante aconselhá-los a não manipular, destruir ou danificar as embalagens.

ATENÇÃO! Aproveite essa oportunidade para pedir que coletem em suas casas conta-gotas sem uso, copos dosadores, colheres medidoras, colheres comuns e copos descartáveis de diferentes tamanhos. Basta uma unidade de cada tipo para cada grupo de 4 alunos. Incentive os alunos a se organizarem para a coleta.

 

2ª parte

Inicialmente, com a classe organizada em grupos e com as anotações obtidas na pesquisa de rótulos de medicamentos, peça que analisem o que os colegas trouxeram e verifiquem entre eles se aparece algo diferente do que foi apresentado na primeira etapa dessa atividade.

Eventualmente, eles trarão outras unidades de medida, como micrograma (µg), e informações de medicamentos em comprimidos ou pastilhas com anotações apenas de medidas em gramas ou miligramas.

Evite dar respostas imediatas e faça-os pensar sobre cada caso, com boas perguntas, como:

• Vocês sabem o que é um miligrama (mg)? O que acham que poderia ser um micrograma (µg)? Deve ser maior ou menor que um miligrama? Quanto?
• Por que não é preciso mostrar mais informações sobre um comprimido ou pastilha do que a sua massa?

Oriente-os a buscar respostas na internet ou com colegas que dizem saber responder.

Ao final, se for preciso, sistematize as seguintes informações:

Um miligrama (cuja abreviação é mg) corresponde à milésima parte do grama ou 1/1.000 g. Um micrograma (cuja abreviação se faz com a letra gregra mícron, µg) equivale à milionésima parte do grama ou 1/1.000.000 g. Um nanograma (ng) é ainda menor: equivale a 1/10⁹ g.

Quanto aos comprimidos, é informada a massa do ou dos componentes ativos em cada um. Assim, um mesmo medicamento pode ser apresentado com dosagens diferentes, por exemplo, 25 mg, 50 mg ou 100 mg, significando que esses são os valores da massa do componente ativo do medicamento em cada comprimido.

 

3ª parte

Nessa parte da atividade, vamos propor um jogo de estimativas de medidas de capacidade. O objetivo é mostrar aos alunos que, assim como é importante estimar o valor de medidas de comprimento ou área para quem trabalha com medicamentos e dosagens, é essencial ter alguma estimativa de valores de capacidade, pois ajuda a reduzir erros.

É importante nessa etapa que eles já tenham coletado sucata, colheres, conta-gotas e copinhos dosadores.

Veja se é possível que os alunos tragam conta-gotas de medicamentos com o prazo de validade vencido e as embalagens devidamente lavadas, vale o mesmo para colheres ou copinhos dosadores.

 

 

Verifique se eles conseguem copos medidores com marcações em mL ou se existe esse tipo de material no laboratório da escola.

 

 

Nessa parte da atividade, vamos propor um jogo de estimativas de medidas de capacidade. O objetivo é mostrar aos alunos que, assim como é importante estimar o valor de medidas de comprimento ou área para quem trabalha com medicamentos e dosagens, é essencial ter alguma estimativa de valores de capacidade, pois ajuda a reduzir erros.

Questione:

• Vocês têm ideia de quanto é 1 mL? Onde essa unidade de medida aparece?
• Vocês já tomaram xarope ou medicamento para febre? Usaram copinhos medidores? Quantos mL de xarope cabem em um desses copinhos medidores?
• Tomar 30 gotas de medicamento para febre é o mesmo que tomar uma colher de chá desse remédio?

Deixe que façam suas hipóteses e proponha que se organizem em grupos de 4 alunos, com um conjunto de recipientes, colheres, copos descartáveis e, se possível, conta-gotas, copinhos dosadores em cada grupo e água em uma garrafa PET.

Em seguida, apresente as regras do jogo. Deixe que leiam e só depois pergunte se eles têm alguma dúvida. Esclareça o que for preciso para que eles possam jogar com tranquilidade.

 

JOGO – Estimar é importante!

Organizem-se em quartetos, dupla contra dupla.

Para o quarteto, vocês precisam de: recipientes diversos, colheres, copinhos descartáveis, copos dosadores, conta-gotas e uma garrafa grande com água.

Regras:

1. Uma dupla joga contra a outra e vocês decidem qual delas começa a jogar.
2. A primeira dupla escolhe dois dos objetos do grupo e pede que a outra estime quantas vezes o menor deles cabe no outro, ou melhor, quantas vezes o maior tem a capacidade do menor. Por exemplo: se vocês têm colher de chá e copinho descartável de café, podem perguntar quantas colheres enchem o copinho.
3. A dupla desafiada deve fazer a estimativa e registrar o valor escolhido na folha de papel. Depois, fazem a comparação usando água e verificam a medida correta, que também deve ser anotada.
4. Os pontos da dupla nessa jogada é a diferença entre o valor estimado e o valor real.
5. A seguir, a segunda dupla desafia a primeira, e assim por diante, até que cada dupla faça 5 estimativas e 5 medições exatas.
   Veja um exemplo:

1. Ao final, ganha a dupla que conseguir menos pontos no total das 5 jogadas.

Cuidado nas estimativas. Bom jogo!

 

Observe os grupos enquanto jogam. Essa é uma excelente oportunidade para você observar e avaliar seus alunos.

Ao final do jogo, faça uma roda de conversa e pergunte se eles se saíram bem ou não em suas estimativas e se agora têm alguma noção mais apurada de quanto é um mL.

Comente com a classe que as dosagens de medicamentos administrados por gotejamento – como soro, remédios para dores intensas e alimentação de pacientes muito debilitados – envolvem medições que relacionam gotas e soluções em mililitros. Diga aos alunos que, na próxima etapa da atividade, eles verão alguns tipos dessas dosagens. Assim, conhecerão um pouco da matemática que profissionais da saúde precisam dominar para a administração de medicamentos.

 

4ª parte

Como anunciado aos alunos, agora eles resolverão problemas típicos do cotidiano da enfermagem. Apresente então os seguintes problemas que podem ser resolvidos em duplas com apoio da calculadora, uma vez que o objetivo é não é a resposta, mas o desenvolvimento do pensamento proporcional.

 

PROBLEMAS

Com seu colega de dupla, resolva agora os seguintes problemas que fazem parte do cotidiano de profissionais da enfermagem.

Problema 1

O médico prescreveu 500 mg de Keflex intravenoso de 6 em 6 horas. No posto de enfermagem há frascos de 60 mL de Keflex a 250 mg/5 mL. Quantos mL devem ser administrados no paciente a cada aplicação?

Problema 2

Quantos gramas de bicarbonato de sódio são necessários para preparar 1000 mL de solução a 5%?

Problema 3

A dose prescrita pelo pediatra de um certo medicamento é de 50mg/kg/dia a ser dada de 12/12 horas. Sabendo que a criança pesa 20kg e o frasco é de 250mg/5ml, quantos ml serão dados por horário?

DICA: divida a resolução em: cálculo da dose diária; cálculo da dose por horário; e, finalmente, quantos mL por horário.

No próximo problema será necessário diluir o medicamento, pois a concentração pedida é menor do que a que está disponível, isso pode ser feito diluindo o medicamento disponível em água destilada. Vamos ver como vocês resolvem essa situação?!

Problema 4

É preciso administrar 2.000.000 UI de penicilina cristalina por via endovenosa de 4 em 4 horas. O frasco ampola disponível é de 5.000.000 UI em 2 mL. Quanto deve ser aplicado ao paciente?

 

Acompanhe o trabalho das duplas e registre as dúvidas e aprendizagens dos alunos em seu caderno de bordo.

Termine com um painel de soluções. É natural que os alunos tenham muitas dúvidas, afinal esse não é o dia a dia deles e muitos termos são ainda novos para eles. O importante não é a resposta correta, mas o entendimento de que a matemática permeia essa profissão e respostas exatas são aqui muito importantes, pois delas depende a saúde ou a vida de pessoas.

 

 

 

---

Respostas dos problemas

Problema 1

O frasco disponível tem 250 mg em 5 mL da solução, a prescrição médica é de 500 mg, logo, deve administrado o dobro de 5 mL da solução. A resposta é 10 mL.

Problema 2

Como 5% de 1000 é 50, para obter a solução a 5%, devemos ter 50 mg de bicarbonato de sódio em 1000 mL da solução.

Problema 3

Cálculo da dose diária: multiplicamos a dose pelo peso.
Dose diária = 50 x 20 = 1000 mg por dia.

Cálculo da dose por horário: divide-se a dose diária pelo número de doses ao dia (duas ao dia).
Dose por horário = 500 mg por horário.

Cálculo de quantos mL por horário, fazendo regra de 3:
250 mL———————- 5 mL
500 mg——————— x mL
x = 10 mL por horário.

Problema 4

Esse problema pode ser resolvido por regra de três simples sem diluição, assim:
5.000.000 UI ————— 2 mL
2.000.000 UI ————— x mL
e temos x = 0,8 mL, no entanto essa precisão em seringas é muito difícil de ser conseguida, por isso a indicação de diluir e obter quantidade maior em seringas padronizadas.

Diluindo as 5.000.000 UI do medicamento em mais 8 mL de água destilada, temos:
2 mL da embalagem original + 8 mL de água destilada = 10 mL de solução.

Temos, então:
5.000.000 UI ——— 10 mL
2.000.000 UI ——— x mL calculando x = 4 mL, quantidade da solução a ser administrada para atender ao pedido médico.