
A Geometria está presente no cotidiano do estudante (no corpo, na natureza, em obras de arte, em construções, etc.) e constitui parte importante do currículo de Matemática a partir dos anos iniciais do Ensino Fundamental. A sua compreensão envolve a capacidade de comparar, observar regularidades, levantar e validar/descartar hipóteses, de abstrair e generalizar. Desta forma, o estudo da Geometria também contribui com as outras unidades temáticas.
Apesar da relevância do trabalho com Geometria nas aulas de Matemática, historicamente ele representa um grande desafio. Se por um lado muitas vezes não recebe a devida importância e fica para o fim do ano, sendo abordado de forma superficial, por outro, às vezes, fica perdido em meio a atividades repetitivas cujos objetivos limitam-se a desenhar e nomear formas geométricas.
Frente a esses desafios, esse artigo apresenta algumas reflexões sobre o ensino e a aprendizagem de um tema abordado na unidade temática Geometria, que muitas vezes é trabalhado apenas de forma intuitiva nos anos iniciais do Ensino Fundamental: as transformações geométricas, em especial, a simetria de reflexão (ou simetria axial). Esse tema ganha força nesse segmento com a implementação da Base Nacional Comum Curricular (BNCC). Segundo o documento, as ideias matemáticas fundamentais associadas a essa temática são, principalmente, a construção, a representação e a interdependência de figuras.
A Geometria envolve o estudo de um amplo conjunto de conceitos e procedimentos necessários para resolver problemas do mundo físico e de diferentes áreas do conhecimento. Assim, nessa unidade temática, estudar posição e deslocamentos no espaço, formas e relações entre elementos de figuras planas e espaciais pode desenvolver o pensamento geométrico dos alunos. Esse pensamento é necessário para investigar propriedades, fazer conjecturas e produzir argumentos geométricos convincentes. É importante, também, considerar o aspecto funcional que deve estar presente no estudo da Geometria: as transformações geométricas, sobretudo as simetrias. As ideias matemáticas fundamentais associadas a essa temática são, principalmente, construção, representação e interdependência. (BRASIL, 2017, p. 267)
Ao estudar simetria de reflexão, o estudante identifica a manutenção de formas, distâncias, comprimentos e aberturas (ângulos), pois o reconhecimento dessas propriedades em figuras e em pares de figuras contribui para a construção de um conceito muito importante da geometria: a congruência. Vale lembrar que é muito comum o estudante relacionar o conceito de congruência ao de igualdade, porém ser congruente não é ser igual, mas ter o mesmo tamanho, a mesma forma e as mesmas de aberturas de ângulos. Veja o exemplo:
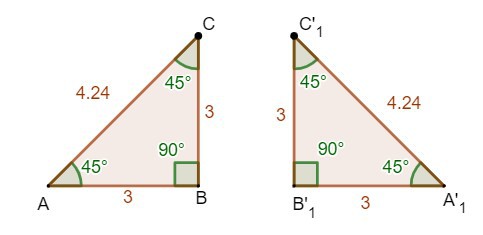
As duas figuras geométricas ABC e A1B1C1 representadas ao lado possuem a mesma forma e o mesmo tamanho: lados correspondentes com a mesma medida e ângulos correspondentes também com a mesma medida, porém elas não são iguais, e sim, congruentes.
É notório que existem diferentes recursos para iniciar o estudo da simetria: malha quadriculada, dobradura, espelho, geoplano, software de geometria dinâmica… Porém não é apenas essa diversidade que contribui com a aprendizagem. É preciso tomar cuidado para não transformar o estudo da simetria em um conjunto de atividades repetitivas que, embora utilizem recursos diferentes, possuem o mesmo objetivo: desenhar figuras simétricas. A intencionalidade do professor precisa ir além das atividades práticas com recursos diversificados, o seu papel é fundamental: fazer boas perguntas, levar o estudante a observar as construções realizadas, perceber regularidades, formalizar conceitos e fazer generalizações. É importante, também, estimular a criança não só a observar, mas verbalizar as suas conclusões, utilizando vocabulário matemático adequados.
HOFFER (1981) afirma que há habilidades de percepção que precisam ser desenvolvidas pelo estudante enquanto explora as transformações geométricas, como a simetria de reflexão. São elas:
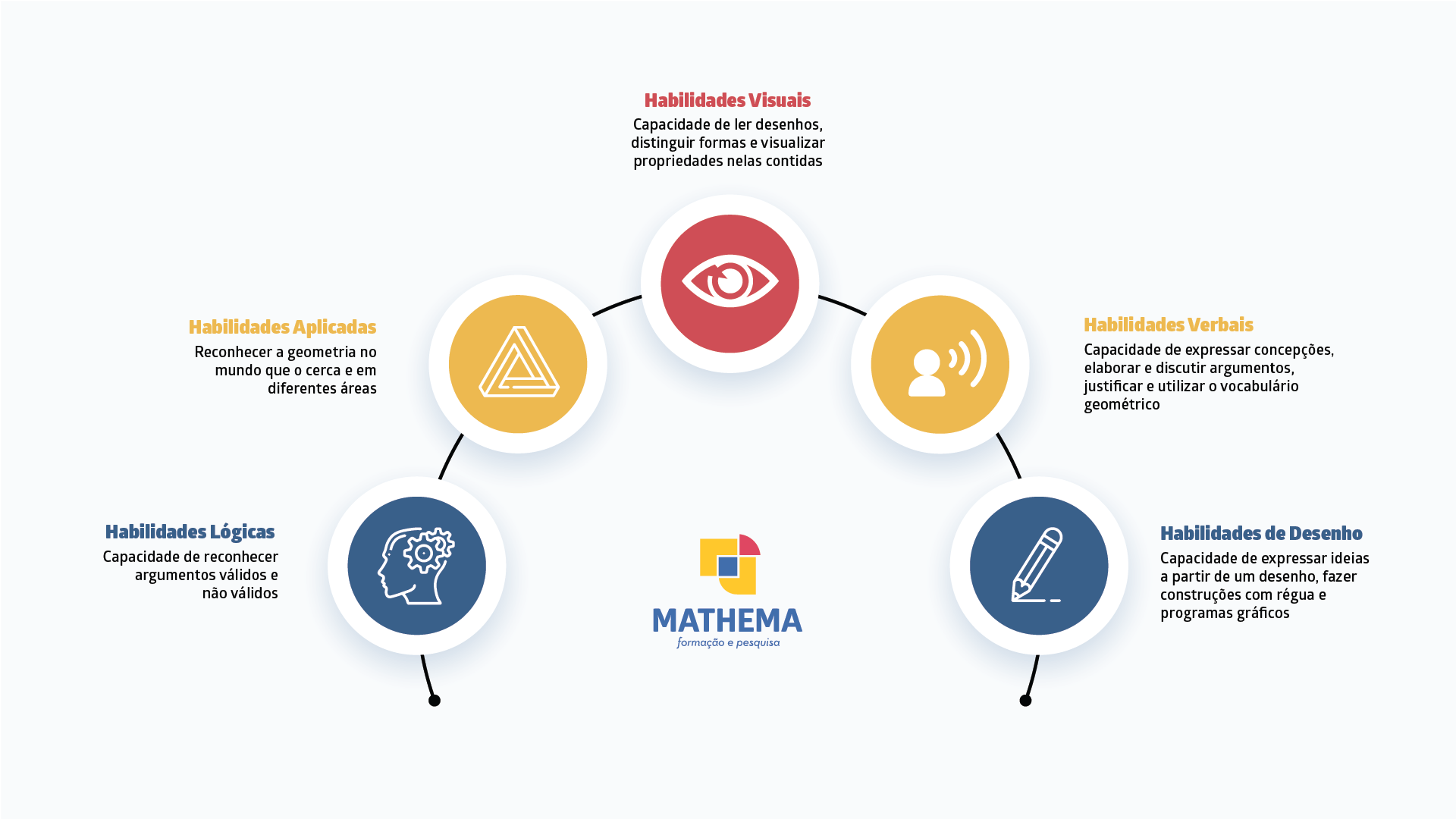
As habilidades visuais, verbais, de desenho, lógica e aplicadas estão relacionadas ao desenvolvimento do pensamento geométrico do estudante e são fundamentais no seu processo de formação.
Para desenvolver o pensamento geométrico, o professor pode, por exemplo, iniciar a atividade com uma roda de conversa, fazendo boas perguntas, para que o estudante formule hipóteses antes mesmo de realizar o desenho. Uma sugestão: proponha uma atividade para desenhar uma figura simétrica à figura dada em uma malha quadriculada.
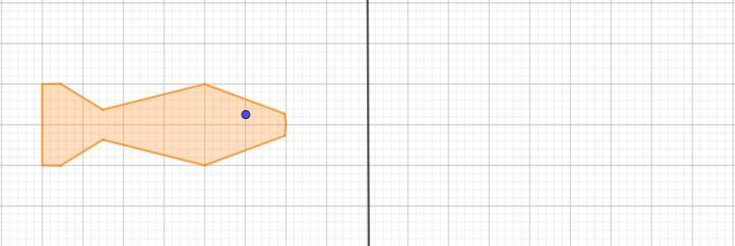
Observe a figura do peixinho. Você fará uma figura simétrica a essa, considerando que a linha desenhada funcionará como um espelho (essa linha recebe o nome de eixo de simetria).
Depois da roda de conversa, os estudantes desenham a figura simétrica e, para finalizar a atividade, o professor retoma as hipóteses formuladas na roda de conversa e discute se elas foram confirmadas ou não.
Atividades como essa vão além de desenhar figuras simétricas. Essas boas perguntas contribuem para o desenvolvimento da percepção visual do estudante, na qual ela “imagina” o resultado do movimento, argumenta, formula hipóteses que serão checadas após a realização do desenho e desenvolve o vocabulário geométrico.
Diante das reflexões apresentadas neste artigo, acreditamos que há muito o que avançar no ensino de simetria de reflexão, visto que esse tema muitas vezes é abordado de forma superficial nos anos iniciais, predominando apenas o seu caráter intuitivo em detrimento ao desenvolvimento do pensamento geométrico. Enfatizamos a importância da intencionalidade do professor em ir além de atividades práticas, e apresentar situações que levem o estudante a observar, argumentar e verbalizar suas descobertas.
Pensando nisso, elaboramos uma atividade que tem como objetivo abordar o estudo da simetria de uma forma um pouco mais aprofundada. Escolhemos utilizar como recurso um software de geometria dinâmica: o Geogebra. Quando bem explorado, ele incentiva a criatividade, a exploração de conceitos, a descoberta.
Concordamos com GRAVINA (1996) quando ele afirma que: o uso de softwares de geometria dinâmica possibilita que o estudante experimente, crie estratégias, faça conjecturas, argumente e deduza sobre os conceitos e propriedades matemáticas. Acreditamos que dessa forma estamos contribuindo com o desenvolvimento do pensamento geométrico do estudante.
Estudo da Simetria utilizando como recurso o Geogebra
Observações iniciais:
Atividade
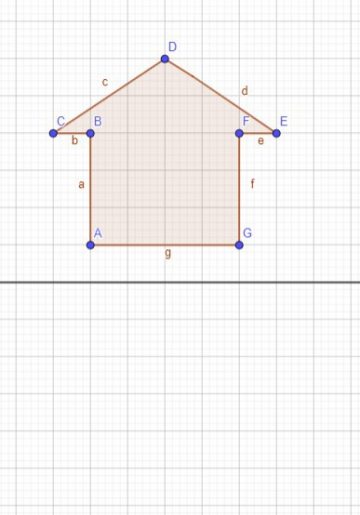
1) Projete um desenho e um eixo de simetria (como a casinha a seguir), e peça para o estudante desenhar uma casinha idêntica utilizando o Geogebra e seguindo os seguintes passos:
i. Selecione a ferramenta “Polígono”1, disponível na quarta janela da barra de ferramentas. Depois, na malha quadriculada, utilizando o botão esquerdo do mouse, clique em cada ponto ou vértice desejado.
ii. Selecione a ferramenta “Reta”, disponível na terceira janela da barra de ferramentas e construa uma reta horizontal abaixo da figura, conforme a figura projetada.
2) Selecione a ferramenta “Polígono”1, disponível na quarta janela da barra de ferramentas. Depois, na malha quadriculada, utilizando o botão esquerdo do mouse, clique em cada ponto ou vértice desejado.
3) Selecione a ferramenta “Reta”, disponível na terceira janela da barra de ferramentas e construa uma reta horizontal abaixo da figura, conforme a figura projetada.
4) O próximo passo é uma nova roda de conversa com boas perguntas: Qual estratégia utilizaram para obter o polígono/casinha simétrica? Quais as semelhanças entre os dois polígonos? Quais as diferenças? Depois da conversa, peça aos estudantes que observem as construções dos colegas e identifiquem semelhanças e diferenças com a sua construção.
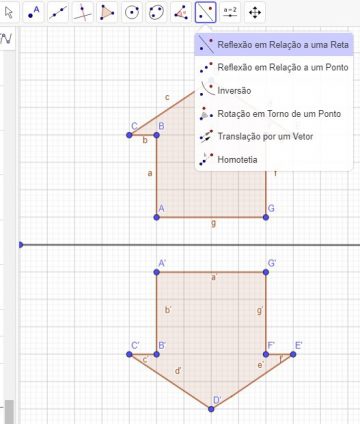
5) Para finalizar, explique que esse software tem um recurso que constrói polígonos simétricos a um polígono dado, e peça para a criança utilizar esse recurso no polígono que ele desenhou primeiro.
i. Selecione a ferramenta “Reflexão em Relação a uma Reta”, disponível na 9a janela da barra de ferramentas. Em seguida, clique em qualquer lugar dentro do 1o polígono desenhado.
ii. Depois, clique sobre o eixo de simetria e logo a figura simétrica aparecerá.
6) Se o estudante aplicou os conceitos de simetria corretamente, as figuras ficarão sobrepostas, mas em um “tom” um pouco mais escuro. Caso ela tenha errado, surgirá a figura correta, que não ficará sobreposta àquela que ele construiu. Nesse momento, é importante discutir porque as figuras não ficaram sobrepostas, quais são os vértices marcados em lugar incorreto, qual deveria ser a distância entre o ponto incorreto e o eixo de simetria? Por quê?
7) Para finalizar, faça um levantamento coletivo das principais características da simetria de reflexão.
É esperado que ao término da atividade, os estudantes concluam que na simetria a forma, o comprimento dos lados, a abertura dos ângulos do polígono e as distâncias ao eixo de simetria sempre se conservam, mas a posição do polígono muda. É importante estimulá-los a verbalizar essas observações.
1 Professor, você pode conversar com as crianças sobre o que é polígono: figura fechada, formada por linhas retas que não se cruzam.
Referências
Todos os campos devem ser preenchidos.
Seu e-mail não será publicado.
Muito bom,ideias maravilhosas,adorei.
Ótimo material
Muito interessante, pois mostra como podemos trabalhar geometria com os alunos, além de indicar sofware como o geogebra que pode ser trabalhados em aula.
No momento em que estamos vigendo, aprender e trabalhar com ferramentas digitais dentro da sala de aula torna a aula mais atrativa
Acho importante usa-lo em sala de aula este aplicativo da geogebra.
Esse texto é muito produtivo, pois ajuda o professor que está iniciando sua carreira docente. Mostra que a geometria vai além da simples figura geométrica e ajuda o professor a conduzir o aluno ao pensamento lógico, ao desenvolvimento da fala e habilidades na construção através dos erros e acertos chegando ao objetivo esperado.
Método da Aprendizagem tem como propósito tornar o aluno capaz de construir o aprendizado conceitual, procedimental e atitudinal por meio de problemas propostos que o expõe a situações motivadoras e o prepara para o mundo do trabalho.
Achei muito bom esse material,pois traz um a nova versão para o ensino da geometria.O que acho muito importante é a interação do professor fazendo as perguntas e levando os alunos a pensarem sobre o que produziram.Depois fazer a sistematização do conhecimento elaborado com os alunos.
Muito boas as atividades.
muito bom, simples de fácil compreenção.
Ótimo ferramenta para ensino de geometria, recurso de ensino interativo, descontraído e atrativo para os alunos.
Gosto muito de trabalhar com o Geogebra e agora com novas ideias.
Eu gosto muito de usar desenho, além de ajudar na ampliação da visão, contribui muito para coordenação motora fina. O papel quadriculado ou milimetrado é um grande aliado do professor de matemática.
Ótima sugestão